こんにちは。Tama(@tamateur_com)です!
今回は、補数について解説します。
2の補数は、負の値を表現するためや、減算(引き算)をするために使われています。
補数という概念はじめて出会ったときは、全く理解できませんでした。
文章で説明されてもなかなか理解しにくいと思うので、実例をもとに解説していきます!
まずは、Wikipediaの説明を見てみましょう。
補数(ほすう、complement)とは、ある記数法のもとで、ある自然数 a に足したとき桁が1つ上がる(桁が1つ増える)数のうち最も小さい数をいう。
https://ja.wikipedia.org/wiki/%E8%A3%9C%E6%95%B0
記数法とは、N進法とも言われ、10進数や2進数、8進数などのことです。
2の補数の前に、10の補数から解説します。その方がイメージが湧くと思います。
10進数の38の10の補数は、62になります。
38は2桁なので、桁が1つ増える(3桁になる)のは62を足した時だからです。
下の例では②の場合にあたります。
ちなみに、①の場合を9の補数といいます。つまり、桁上がりしない最大の数です。
①38+61=99 ← 2桁で桁上がりしないので、補数ではない。(9の補数)
②38+62=100 ← 3桁に桁上がりし、かつ最小の数なので補数となる。(10の補数)
③38+63=101 ← 3桁に桁上がりしているが、最小の数ではないので補数ではない。
図で表すと下のようになります。

ここから、2進数における補数について解説します。
2進数”1011″の2の補数は、”0101″になります。
“1011”は4桁なので、桁が1つ増える(5桁になる)のは”0100″を足した時だからです。
下の例では②の場合にあたります。
ちなみに、①の場合を1の補数といいます。つまり、桁上がりしない最大の数です。
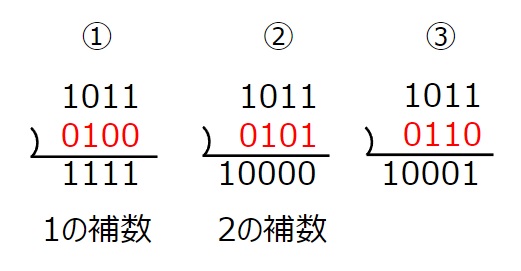
①1011+0100=1111 ← 4桁で桁上がりしないので、補数ではない。(1の補数)
②1011+0101=10000 ← 5桁に桁上がりし、かつ最小の数なので補数となる。(2の補数)
③1011+0110=10001 ← 5桁に桁上がりしているが、最小の数ではないので補数ではない。
図で表すと下のようになります。
これで、2の補数の仕組みが分かったと思います。
試験で出題された時に、素早く2の補数を求めなければいけません。
最後に実際の求め方を解説します。
上の解説で使用した2進数”1011″をもとに解説します。
2進数→1の補数→2の補数 の順番で求めていきます。
手順① 1の補数を求める
1の補数を求めるためには、すべての0と1を反転します。
すると、1011 → 0100になり1の補数の完成です。
どうですか?とても簡単ですよね?
手順② 2の補数を求める
2の補数を求めるためには、1の補数に1を足します。
すると、0100 + 0001 → 0101となり、2の補数の完成です。

このように、補数を求めるだけなら、だれでも出来てしまいます。
試験対策だけなら、これでも良いですが、エンジニアとしてやっていくなら、
仕組みを理解して説明できるようにしておくべきだと思います。
冒頭でも書いたように、補数は、負の値を表現するためや、減算(引き算)をするために使われています。
このような応用的な使い方も順次解説していきたいと思います。